September 15, 2023

Data Structure & Algorithms

Intro to Data Structure & Algorithms

Data Structures are organized ways to store and arrange data so operations (insert, search, delete, traverse) can be performed efficiently. Algorithms are finite, well-defined step-by-step procedures to solve a problem or transform input to output. Together they form the core toolkit for writing software that is not only correct but scalable and maintainable.

Why they matter:

Performance: Choosing the right structure can turn an O(n²) solution into O(n log n) or better.
Resource efficiency: Good space management lowers memory pressure and costs.
Reliability & clarity: Proper abstractions reduce bugs and cognitive load.
Scalability: Enables systems to handle growth in users, data volume, or complexity.

Common data structure families:

Linear: Arrays, Dynamic Arrays, Linked Lists
Hierarchical: Stacks, Queues, Heaps, Priority Queues
Associative / Lookup: Hash Tables, Maps, Sets
Recursive / Hierarchical: Trees (BST, AVL, Red-Black, Trie, Segment, Fenwick)
Graphs: Directed, Undirected, Weighted
Specialized: Disjoint Set (Union-Find), Bloom Filter, LRU Cache patterns

Algorithm paradigms:

Brute Force (baseline)
Divide & Conquer (Merge Sort, Quick Sort)
Greedy (Interval Scheduling, Huffman Coding)
Dynamic Programming (Knapsack, LIS)
Backtracking (N-Queens, Sudoku)
Graph Strategies (BFS, DFS, Dijkstra, Topological Sort)
Probabilistic / Approximation (when exact is expensive)

Measuring efficiency:

Time complexity: Big-O (upper bound), Θ (tight), Ω (lower bound)
Space complexity: Auxiliary memory beyond input
Trade-offs: Faster lookup vs slower updates, memory overhead vs speed

Core goals of a good solution:

Correctness
Clarity
Optimal or acceptable complexity
Predictable behavior under scale
Maintainability and adaptability

Real-world mappings:

Autocomplete: Tries
Social networks: Graph traversals
Feed ranking: Heaps / priority queues
Caches & sessions: Hash maps + eviction policies
Conflict detection / geometry: Segment Trees / Interval Trees
Compilers / interpreters: Abstract syntax trees

Mindset:

Define the problem precisely (inputs, outputs, constraints).
Identify dominant operations (reads, writes, lookups, aggregations).
Estimate growth (n, m, depth, frequency).
Choose structure → validate with complexity → prototype → measure.

A Priori Analysis vs A Posteriori Testing

Understanding performance has two complementary angles:

A priori (theoretical) analysis:

Done before (or without) running code.
Abstract machine model: count primitive operations (comparisons, assignments, hash lookups).
Express cost as a function of input size n (and other parameters: m edges, k keys, h height).
Derive worst, average, best cases; classify with Big-O / Θ / Ω.
Ignores constant factors, cache effects, language/runtime overhead.
Useful for design decisions, comparing alternative data structures, spotting impossible scalability.

A posteriori (empirical) testing:

Run real (or synthetic) inputs and measure.
Metrics: wall time, CPU time, allocations, memory peak, cache misses, branch mispredicts (if profiled), throughput, latency distribution (p50/p95/p99).
Tools: benchmark harnesses, profilers, tracing, instrumentation counters.
Reveals constant factors, hidden costs (boxing, GC, I/O), micro-architectural impacts.
Validates (or falsifies) theoretical assumptions with real data distributions.

Why both matter:

Theory filters out fundamentally non-scalable designs early.
Measurement prevents overconfidence in asymptotics (e.g., O(n) with huge constant vs tuned O(n log n)).
Discrepancies highlight modeling gaps (e.g., hash collisions, poor branching, memory locality).

Recursion

Definition and Core Concept

Recursion is a programming technique where a function calls itself to solve a smaller instance of the same problem. It's based on the mathematical principle of mathematical induction. Key Components:

Recursive Case: The function calls itself with a modified parameter Base Case: A condition that stops the recursion (prevents infinite calls)

How Recursion Works

The Call Stack

When a function calls itself:

Each function call is pushed onto the call stack
Parameters and local variables are stored for each call
When a base case is reached, functions start returning
The stack "unwinds" as each function completes

Memory Model

factorial(4)
  └── factorial(3)
      └── factorial(2)
          └── factorial(1)  ← Base case reached
              └── returns 1
          ← returns 2 * 1 = 2
      ← returns 3 * 2 = 6
  ← returns 4 * 6 = 24

Anatomy of a Recursive Function

def recursive_function(parameters):
    # Base case(s) - ALWAYS check first
    if base_condition:
        return base_value
    
    # Recursive case - problem reduction
    # Must move toward base case
    return some_operation(recursive_function(modified_parameters))

Essential Elements:

Progress toward base case: Each recursive call must bring you closer to the base case
Problem decomposition: Break the problem into smaller, similar subproblems
Combine results: Use the result of smaller problems to solve the larger one

Classic Examples

Example 1: Factorial

def factorial(n):
    # Base case
    if n <= 1:
        return 1
    
    # Recursive case
    return n * factorial(n - 1)
# factorial(5) = 5 * 4 * 3 * 2 * 1 = 120

Example 2: Fibonacci Sequence

def fibonacci(n):
    # Base cases
    if n <= 1:
        return n
    
    # Recursive case
    return fibonacci(n - 1) + fibonacci(n - 2)
 
# fibonacci(6) = 8
# Sequence: 0, 1, 1, 2, 3, 5, 8, 13...

Example 3: Binary Tree Traversal

class TreeNode:
    def __init__(self, val=0):
        self.val = val
        self.left = None
        self.right = None
 
def inorder_traversal(root):
    # Base case
    if not root:
        return []
    
    # Recursive case
    left_vals = inorder_traversal(root.left)
    right_vals = inorder_traversal(root.right)
    
    return left_vals + [root.val] + right_vals

Types of Recursion

Linear Recursion: Function calls itself once per execution Examples: factorial, linear search Call stack grows linearly with input size

Binary Recursion: Function calls itself twice per execution Examples: Fibonacci, binary tree traversal Can lead to exponential time complexity

Tail Recursion: Recursive call is the last operation in the function Can be optimized by compilers to avoid stack growth Example:

def tail_factorial(n, accumulator=1):
    if n <= 1:
        return accumulator
    return tail_factorial(n - 1, n * accumulator)

Mutual Recursion: Two or more functions call each other

Example:

def is_even(n):
    if n == 0:
        return True
    return is_odd(n - 1)
 
def is_odd(n):
    if n == 0:
        return False
    return is_even(n - 1)

Recursion vs Iteration

When to Use Recursion:

Tree/Graph structures: Natural recursive structure
Divide and conquer: Problems that break into similar subproblems
Mathematical definitions: When the problem is naturally defined recursively
Backtracking: Exploring multiple solution paths

When to Use Iteration:

Simple counting/accumulation: Loops are more efficient
Stack space concerns: Large inputs might cause stack overflow
Performance critical: Iteration often has less overhead

Comparison Table:

Aspect	Recursion	Iteration
Memory	Uses call stack (O(n) space)	Uses constant space
Speed	Slower (function call overhead)	Faster
Code clarity	Often more readable	Can be more complex for some problems
Stack overflow	Possible with deep recursion	Not an issue

Common Patterns and Applications

Divide and Conquer

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    
    return merge(left, right)

Backtracking

def solve_n_queens(n):
    def backtrack(row, board):
        if row == n:
            solutions.append([''.join(row) for row in board])
            return
        
        for col in range(n):
            if is_safe(board, row, col):
                board[row][col] = 'Q'
                backtrack(row + 1, board)
                board[row][col] = '.'  # backtrack
    
    solutions = []
    board = [['.' for _ in range(n)] for _ in range(n)]
    backtrack(0, board)
    return solutions

Dynamic Programming (with Memoization)

def fibonacci_memo(n, memo={}):
    if n in memo:
        return memo[n]
    
    if n <= 1:
        return n
    
    memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
    return memo[n]

Common Pitfalls and Debugging

Pitfall 1: Missing or Incorrect Base Case

# WRONG - no base case leads to infinite recursion
def bad_factorial(n):
    return n * bad_factorial(n - 1)  # Stack overflow!
 
# WRONG - base case never reached
def bad_countdown(n):
    if n == 0:
        return
    print(n)
    bad_countdown(n + 1)  # n keeps increasing!

Pitfall 2: Not Making Progress

# WRONG - parameter doesn't change
def stuck_function(n):
    if n == 0:
        return 0
    return 1 + stuck_function(n)  # n never decreases!

Pitfall 3: Stack Overflow

Occurs when recursion depth exceeds system limits Python default: ~1000 recursive calls Solutions: Use iteration, tail recursion, or increase recursion limit

Debugging Techniques:

Trace execution: Print parameters at each call
Verify base cases: Ensure they're reachable and correct
Check progress: Confirm parameters move toward base case
Use small inputs: Test with minimal cases first

Performance Analysis

Time Complexity Examples:

Linear recursion (factorial): O(n)
Binary recursion (naive Fibonacci): O(2^n)
Divide and conquer (merge sort): O(n log n)

Space Complexity:

Call stack space: O(depth of recursion)
Tail recursion: O(1) if optimized
With memoization: O(n) additional space

Advanced Concepts

Memoization Pattern

from functools import lru_cache
 
@lru_cache(maxsize=None)
def expensive_recursive_function(n):
    if n <= 1:
        return n
    return expensive_recursive_function(n-1) + expensive_recursive_function(n-2)

Converting Recursion to Iteration

# Recursive
def recursive_sum(arr, index=0):
    if index >= len(arr):
        return 0
    return arr[index] + recursive_sum(arr, index + 1)

Iterative equivalent

def iterative_sum(arr):
    total = 0
    for num in arr:
        total += num
    return total

Parameterized Recursion Using additional parameters to avoid recomputation:

def power_optimized(base, exp, result=1):
    if exp == 0:
        return result
    if exp % 2 == 0:
        return power_optimized(base * base, exp // 2, result)
    else:
        return power_optimized(base, exp - 1, result * base)

Print all subset of a array

def print_subsets(arr):
    def backtrack(index, current_subset):
        if index == len(arr):
            print(current_subset)
            return
        # Include current element
        current_subset.append(arr[index])
        backtrack(index + 1, current_subset)
        current_subset.pop()  # backtrack
        # Exclude current element
        backtrack(index + 1, current_subset)
    backtrack(0, [])
arr = [1, 2, 3]
print_subsets(arr)

Print subsequences whose sum is k

Problem: Given an array and target sum k, find all subsequences that sum to k.

Approach: Use recursion with backtracking. For each element, we have two choices:

Include the element in current subsequence
Exclude the element from current subsequence

def print_subsequences_with_sum_k(arr, k):
    def backtrack(index, current_subsequence, current_sum):
        # Base case: processed all elements
        if index == len(arr):
            if current_sum == k:
                print(current_subsequence)
            return
        
        # Choice 1: Include current element
        current_subsequence.append(arr[index])
        backtrack(index + 1, current_subsequence, current_sum + arr[index])
        current_subsequence.pop()  # backtrack
        
        # Choice 2: Exclude current element
        backtrack(index + 1, current_subsequence, current_sum)
    
    backtrack(0, [], 0)
 
# Example usage
arr = [1, 2, 1]
k = 2
print_subsequences_with_sum_k(arr, k)
# Output: [2], [1, 1]

Recursion Tree for array [1, 2, 1] with k=2:

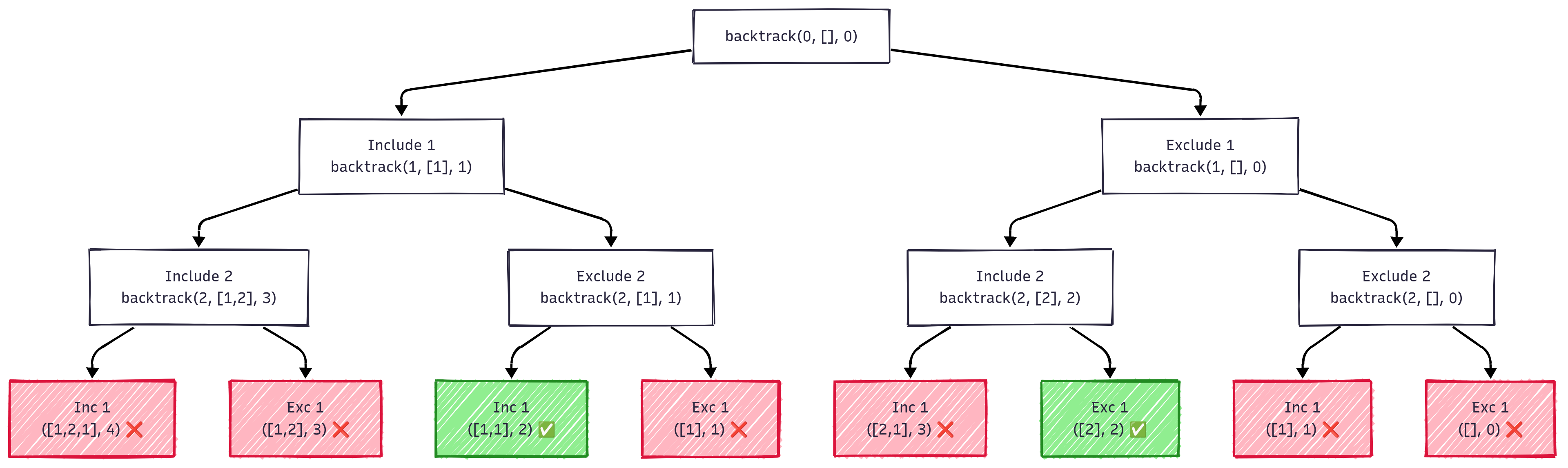
BackTrackVis

Key Points:

Time Complexity: $O(2^n)$ - each element has 2 choices
Space Complexity: $O(n)$ - recursion depth and subsequence storage
Pattern: Classic "include/exclude" decision tree
Optimization: Can add pruning if $current\_sum > k$ (for positive numbers)

Optimized version with pruning:

def print_subsequences_with_sum_k_optimized(arr, k):
    def backtrack(index, current_subsequence, current_sum):
        # Pruning: if sum exceeds k, no point continuing (for positive arrays)
        if current_sum > k:
            return
            
        if index == len(arr):
            if current_sum == k:
                print(current_subsequence[:])  # print copy
            return
        
        # Include current element
        current_subsequence.append(arr[index])
        backtrack(index + 1, current_subsequence, current_sum + arr[index])
        current_subsequence.pop()
        
        # Exclude current element  
        backtrack(index + 1, current_subsequence, current_sum)

Count the Subsequences with Sum k

def count_subsequences_with_sum_k(arr, k):
    def backtrack(index, current_sum):
        if index == len(arr):
            return 1 if current_sum == k else 0
        # Include current element
        count_including = backtrack(index + 1, current_sum + arr[index])
        # Exclude current element
        count_excluding = backtrack(index + 1, current_sum)
        return count_including + count_excluding
    return backtrack(0, 0)
# Example usage
arr = [1, 2, 1]
k = 2
print(count_subsequences_with_sum_k(arr, k))  # Output: 2

Combination of Subsequences with Sum k

To find all combinations of subsequences that sum to k, we can modify our approach to collect valid subsequences instead of just counting them.

def find_combinations_with_sum_k(arr, k):
    def backtrack(index, current_subsequence, current_sum):
        if current_sum == k:
            print(current_subsequence)
            return
        if index == len(arr) or current_sum > k:
            return
        # Include current element
        current_subsequence.append(arr[index])
        backtrack(index + 1, current_subsequence, current_sum + arr[index])
        current_subsequence.pop()
        # Exclude current element
        backtrack(index + 1, current_subsequence, current_sum)
    backtrack(0, [], 0)
# Example usage
arr = [1, 2, 1]
k = 2
find_combinations_with_sum_k(arr, k)

Print all Permutations of a String/Array

def print_permutations(s):
    def backtrack(path, remaining):
        if not remaining or len(path) == len(s):
            print(''.join(path))
            return
        for i in range(len(remaining)):
            path.append(remaining[i])  # Choose
            backtrack(path, remaining[:i] + remaining[i+1:])   # Explore
            path.pop()  # Un-choose
    backtrack([], list(s))

Optimized solution with swapping to avoid extra space:

def print_permutations_optimized(s):
    def backtrack(start):
        if start == len(s) - 1:
            print(''.join(s))
            return
        for i in range(start, len(s)):
            s[start], s[i] = s[i], s[start]  # swap
            backtrack(start + 1)
            s[start], s[i] = s[i], s[start]  # backtrack (swap back)
    s = list(s)
    backtrack(0)
print_permutations_optimized("ABC")

Best Practices

Do:

✅ Always define clear base cases first
✅ Ensure each recursive call progresses toward the base case
✅ Use memoization for overlapping subproblems
✅ Consider iterative solutions for simple cases
✅ Test with small inputs first

Don't:

❌ Forget the base case
❌ Create infinite recursion
❌ Use recursion for simple iteration tasks
❌ Ignore stack overflow possibilities
❌ Modify global state without careful consideration

Binary Search

Binary search is a highly efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing the search interval in half. If the value of the search key is less than the item in the middle of the interval, the search continues in the lower half, or if it's greater, in the upper half. This process repeats until the value is found or the interval is empty.

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    
    while left <= right:
        mid = left + (right - left) // 2
        
        if arr[mid] == target:
            return mid  # Target found
        elif arr[mid] < target:
            left = mid + 1  # Search in the right half
        else:
            right = mid - 1  # Search in the left half
            
    return -1  # Target not found

Binary Search Recursively:

def binary_search_recursive(arr, target, left, right):
    if left > right:
        return -1  # Target not found
    
    mid = left + (right - left) // 2
    
    if arr[mid] == target:
        return mid  # Target found
    elif arr[mid] < target:
        return binary_search_recursive(arr, target, mid + 1, right)  # Search in the right half
    else:
        return binary_search_recursive(arr, target, left, mid - 1)  # Search in the left half

Time Complexity: O(log n) - Each step reduces the search space by half.

Tree Data Structure

A tree is a hierarchical data structure consisting of nodes, where each node contains a value and references to its child nodes. The topmost node is called the root, and nodes without children are called leaves. Trees are widely used in computer science for various applications, including representing hierarchical data, facilitating fast search operations, and organizing data for efficient access.

Types of Trees

Binary Tree: Each node has at most two children (left and right).
Binary Search Tree (BST): A binary tree where the left child's value is less than the parent's value, and the right child's value is greater.
Full Binary Tree: Every node has either 0 or 2 children.
Complete Binary Tree: All levels are fully filled except possibly the last, which is filled from left to right.
Balanced Trees: Trees that maintain a balanced height to ensure efficient operations (e.g., AVL Tree, Red-Black Tree).
Trie: A tree used for storing a dynamic set of strings, where each node represents a character.
Heap: A complete binary tree that satisfies the heap property (max-heap or min-heap).
Segment Tree: A tree used for storing intervals or segments, allowing efficient range queries and updates.

A Tree is typically traversed in two ways:

Breadth First Traversal (Or Level Order Traversal)
Depth First Traversals
- Inorder Traversal (Left-Root-Right)
- Preorder Traversal (Root-Left-Right)
- Postorder Traversal (Left-Right-Root)

Inorder Traversal of Binary Tree

Inorder traversal visits nodes in the following order: left subtree, root node, right subtree. This traversal method is particularly useful for binary search trees (BSTs) because it retrieves values in sorted order.

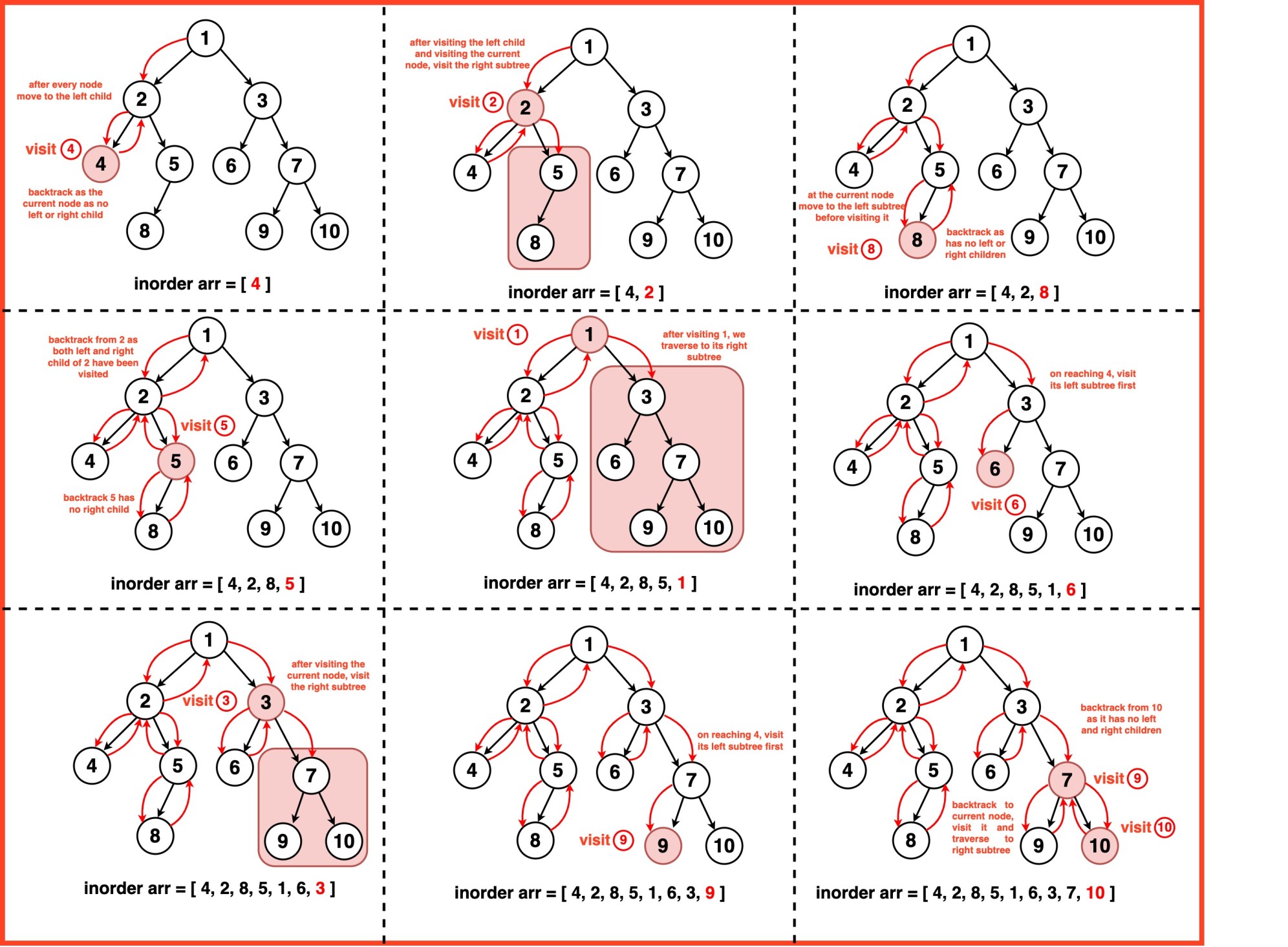
Inorder Traversal

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key
 
def inorder_traversal(root):
    if root is None:
        return
    inorder_traversal(root.left)
    print(root.val, end=' ')
    inorder_traversal(root.right)
 
def inorder_traversal_iterative(root):
    stack = []
    current = root
    
    while stack or current:
        while current:
            stack.append(current)
            current = current.left
        current = stack.pop()
        print(current.val, end=' ')
        current = current.right
 
# Example usage:
if __name__ == "__main__":
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
 
    print("Inorder traversal of binary tree is:")
    inorder_traversal(root)  # Output: 4 2 5 1 3

Postorder Traversal of Binary Tree

In postorder traversal, the nodes are recursively visited in this order: left subtree, right subtree, and then the root node. This traversal is particularly useful for deleting trees or evaluating postfix expressions.

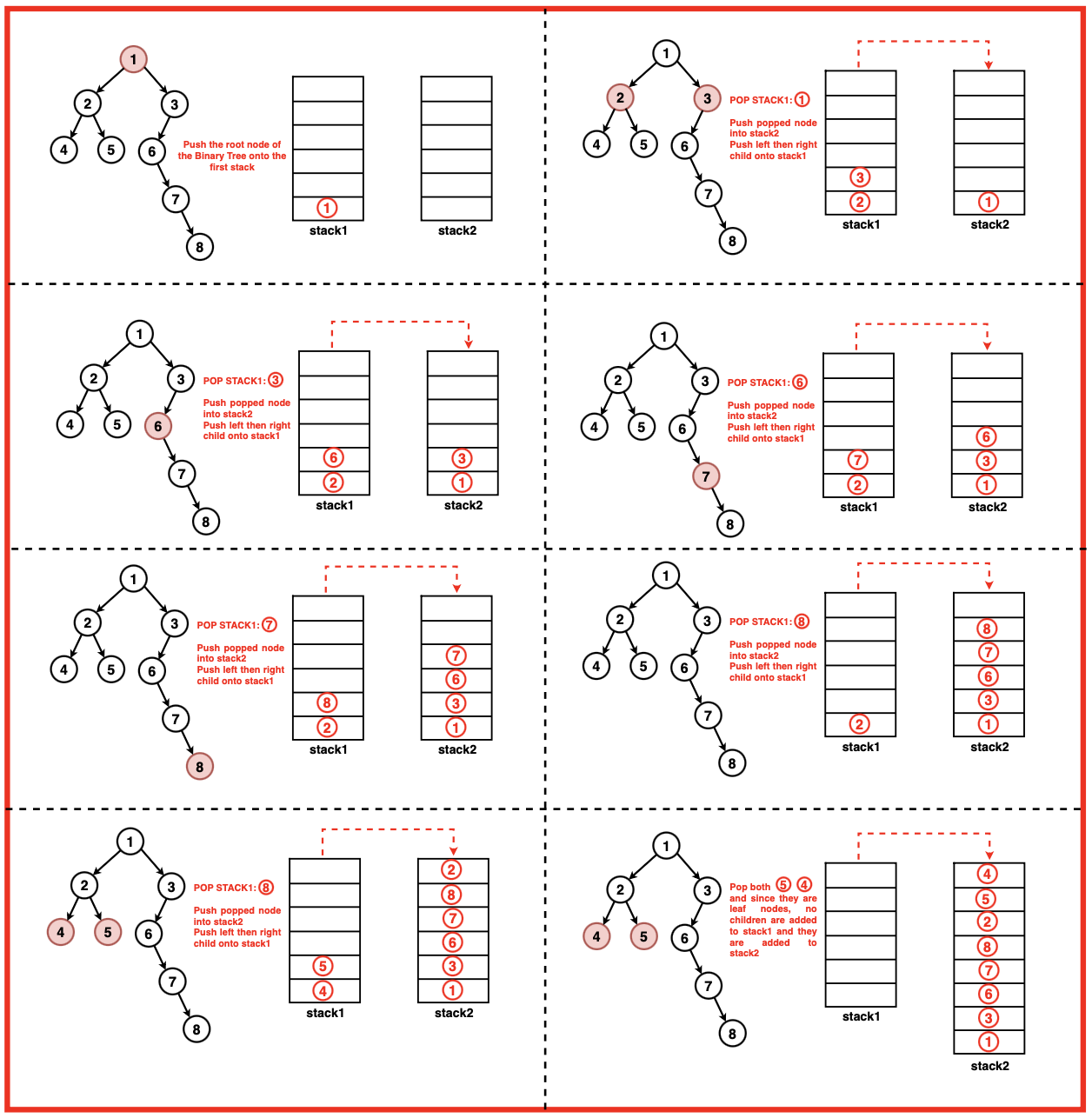
Postorder Traversal

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key
 
def postorder_traversal(root):
    if root is None:
        return
    postorder_traversal(root.left)
    postorder_traversal(root.right)
    print(root.val, end=' ')
 
def postorder_traversal_iterative(root):
    if root is None:
        return
    stack1 = [root]
    stack2 = []
    while stack1:
        node = stack1.pop()
        stack2.append(node)
        if node.left:
            stack1.append(node.left)
        if node.right:
            stack1.append(node.right)
    while stack2:
        node = stack2.pop()
        print(node.val, end=' ')
 
# iterative version using one stack
def postorder_traversal_iterative_one_stack(root):
    if root is None:
        return
    stack = []
    current = root
    while stack or current:
        if current:
            stack.append(current)
            current = current.left
        else:
            temp = stack[-1].right
            if temp is None:
                temp = stack.pop()
                print(temp.val, end=' ')
                while stack and temp == stack[-1].right:
                    temp = stack.pop()
                    print(temp.val, end=' ')
            else:
                current = temp
 
# Example usage:
if __name__ == "__main__":
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    print("Postorder traversal of binary tree is:")
    postorder_traversal(root)  # Output: 4 5 2 3 1

Preorder Traversal of Binary Tree

In preorder traversal, the nodes are recursively visited in this order: root node, left subtree, and then right subtree. This traversal is useful for creating a copy of the tree or for prefix expression evaluation.

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key
 
def preorder_traversal(root):
    if root is None:
        return
    print(root.val, end=' ')
    preorder_traversal(root.left)
    preorder_traversal(root.right)
 
def preorder_traversal_iterative(root):
    if root is None:
        return
    stack = [root]
    while stack:
        node = stack.pop()
        print(node.val, end=' ')
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
 
# Example usage:
if __name__ == "__main__":
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    print("Preorder traversal of binary tree is:")
    preorder_traversal(root)  # Output: 1 2 4 5 3

Height of a Binary Tree

The height of a binary tree is defined as the number of edges on the longest path from the root node to a leaf node. If the tree is empty, the height is -1. If the tree has only one node (the root), the height is 0.

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key
 
def height_of_tree_dfs_recursive(root):
    if root is None:
        return -1  # Height of empty tree is -1
    else:
        left_height = height_of_tree_dfs_recursive(root.left)
        right_height = height_of_tree_dfs_recursive(root.right)
        return max(left_height, right_height) + 1
 
def height_of_tree_bfs_with_depth(root):
    if root is None:
        return -1
    from collections import deque
    queue = deque([(root, 0)])  # (node, current_depth_in_edges)
    max_height = 0
    while queue:
        node, depth = queue.popleft()
        max_height = max(max_height, depth)
        if node.left:
            queue.append((node.left, depth + 1))
        if node.right:
            queue.append((node.right, depth + 1))
    return max_height
 
def height_of_tree_bfs_level_order(root):
    if root is None:
        return -1
    from collections import deque
    queue = deque([root])
    levels = 0
    while queue:
        for _ in range(len(queue)):
            node = queue.popleft()
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        levels += 1
    return levels - 1

Lower bound and Upper bound in a sorted array

Lower Bound: The lower bound of a target value in a sorted array is the index of the first element that is not less than (i.e., greater than or equal to) the target. If all elements are less than the target, it returns the length of the array.
Upper Bound: The upper bound of a target value in a sorted array is the index of the first element that is greater than the target. If all elements are less than or equal to the target, it returns the length of the array.

def lower_bound(arr, target):
    left, right = 0, len(arr)
    while left < right:
        mid = left + (right - left) // 2
        if arr[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left
    
def upper_bound(arr, target):
    left, right = 0, len(arr)
    while left < right:
        mid = left + (right - left) // 2
        if arr[mid] <= target:
            left = mid + 1
        else:
            right = mid
    return left

Segment Tree

A Segment Tree is a binary tree used for storing intervals or segments. It allows querying which of the stored segments contain a given point efficiently. It is particularly useful for answering range queries and performing updates on an array.

class SegmentTree:
    """
    Segment Tree data structure for efficient range queries and updates.
    Supports range sum queries and point updates in O(log n) time.
    """
    
    class Node:
        def __init__(self, start_interval: int, end_interval: int):
            self.data = 0
            self.start_interval = start_interval
            self.end_interval = end_interval
            self.left = None
            self.right = None
        
        def __repr__(self):
            return f"Node([{self.start_interval}-{self.end_interval}], data={self.data})"
    
    def __init__(self, arr: list[int]):
        if not arr:
            raise ValueError("Array cannot be empty")
        self.root = self._construct_tree(arr, 0, len(arr) - 1)
    
    def _construct_tree(self, arr: list[int], start: int, end: int) -> Node:
        """
        Recursively construct the segment tree.
        
        Args:
            arr: Input array
            start: Start index of current segment
            end: End index of current segment
        
        Returns:
            Root node of the constructed subtree
        """
        if start == end:
            # Leaf node
            leaf = self.Node(start, end)
            leaf.data = arr[start]
            return leaf
        
        # Create new node for current segment
        node = self.Node(start, end)
        
        # Avoid potential overflow with this mid calculation
        mid = start + (end - start) // 2
        
        node.left = self._construct_tree(arr, start, mid)
        node.right = self._construct_tree(arr, mid + 1, end)
        node.data = node.left.data + node.right.data
        
        return node
    
    def display(self):
        if self.root:
            self._display(self.root)
    
    def _display(self, node: Node):
        parts = []
        
        if node.left:
            parts.append(f"Interval=[{node.left.start_interval}-{node.left.end_interval}] and data: {node.left.data} => ")
        else:
            parts.append("No left child => ")
        
        # Current node
        parts.append(f"Interval=[{node.start_interval}-{node.end_interval}] and data: {node.data}")
        
        if node.right:
            parts.append(f" <= Interval=[{node.right.start_interval}-{node.right.end_interval}] and data: {node.right.data}")
        else:
            parts.append(" <= No right child")
        
        print(''.join(parts) + '\n')
        
        if node.left:
            self._display(node.left)
        if node.right:
            self._display(node.right)
    
    def query(self, qsi: int, qei: int) -> int:
        """
        Perform range sum query.
        
        Args:
            qsi: Query start index
            qei: Query end index
        
        Returns:
            Sum of elements in range [qsi, qei]
        """
        return self._query(self.root, qsi, qei)
    
    def _query(self, node: Node, qsi: int, qei: int) -> int:
        """
        Recursively perform range query.
        
        Args:
            node: Current node
            qsi: Query start index
            qei: Query end index
        
        Returns:
            Sum for the queried range
        """
        # Node completely lies inside query range
        if node.start_interval >= qsi and node.end_interval <= qei:
            return node.data
        
        # Node completely outside query range
        if node.start_interval > qei or node.end_interval < qsi:
            return 0
        
        # Partial overlap - query both children
        return self._query(node.left, qsi, qei) + self._query(node.right, qsi, qei)
    
    def update(self, index: int, value: int):
        """
        Update value at a specific index.
        
        Args:
            index: Index to update
            value: New value
        """
        self._update(self.root, index, value)
    
    def _update(self, node: Node, index: int, value: int) -> int:
        """
        Recursively update the value at given index.
        
        Args:
            node: Current node
            index: Index to update
            value: New value
        
        Returns:
            Updated data value for current node
        """
        # Check if index lies in current node's range
        if index >= node.start_interval and index <= node.end_interval:
            # Leaf node - update the value
            if index == node.start_interval and index == node.end_interval:
                node.data = value
                return node.data
            
            # Internal node - update children and recalculate
            left_ans = self._update(node.left, index, value)
            right_ans = self._update(node.right, index, value)
            node.data = left_ans + right_ans
            return node.data
        
        return node.data
 
if __name__ == "__main__":
    # Create segment tree
    arr = [1, 3, 5, 7, 9, 11]
    seg_tree = SegmentTree(arr)
    
    print("Segment Tree Structure:")
    seg_tree.display()
    
    # Query examples
    print("\n--- Range Queries ---")
    print(f"Sum of range [1, 4]: {seg_tree.query(1, 4)}")  # 3+5+7+9 = 24
    print(f"Sum of range [0, 2]: {seg_tree.query(0, 2)}")  # 1+3+5 = 9
    
    # Update example
    print("\n--- Update Operation ---")
    print(f"Updating index 2 from {arr[2]} to 10")
    seg_tree.update(2, 10)
    
    print(f"Sum of range [1, 4] after update: {seg_tree.query(1, 4)}")  # 3+10+7+9 = 29
    print(f"Sum of range [0, 2] after update: {seg_tree.query(0, 2)}")  # 1+3+10 = 14

Greedy Methods and Algorithms

Fundamental Concepts and Definition

What are Greedy Algorithms?

Greedy algorithms are a class of algorithms that solve optimization problems by making locally optimal choices at each step, with the hope of finding a global optimum. The term "greedy" reflects the algorithm's myopic behavior - it grabs the best immediate option without considering future consequences. Programiz

Formal Definition: A greedy algorithm constructs a solution $S = \{s_1, s_2, \dots, s_n\}$ to an optimization problem by iteratively selecting elements $s_i$ that maximize (or minimize) some criterion function at each step $i$ , without reconsidering previous choices.

Core Principles The greedy paradigm operates on three fundamental principles:

Incremental construction: Solutions are built piece by piece
Irrevocable decisions: Once a choice is made, it cannot be undone
Local optimization: Each decision optimizes based on current state only

Essential Properties of Greedy Algorithms

Deterministic Nature: Given the same input and selection criteria, a greedy algorithm always produces the same output, making it predictable and analyzable. No Backtracking: Unlike exhaustive search or dynamic programming, greedy algorithms never reconsider or modify previous decisions. This property leads to their efficiency but can also result in suboptimal solutions for certain problems. Simple Decision Rules: Greedy algorithms typically employ straightforward selection criteria such as:

Maximum or minimum value selection
Earliest or latest time selection
Highest ratio or density selection
Shortest or longest distance selection

Memory Efficiency: Most greedy algorithms require minimal auxiliary space, often $O(1)$ or $O(n)$ , as they don't need to store multiple solution states or subproblem results.

Algorithmic Characteristics

The general structure of a greedy algorithm follows this pattern:

GREEDY-ALGORITHM(problem_instance):
    solution = ∅
    candidates = INITIALIZE-CANDIDATES(problem_instance)
    
    while solution is not complete and candidates ≠ ∅:
        x = SELECT-BEST(candidates)
        candidates = candidates - {x}
        if FEASIBLE(solution U {x}):
            solution = solution U {x}
    
    return solution

The Greedy Choice Property

Definition: A global optimum can be arrived at by making locally optimal (greedy) choices.

Formal Statement: For an optimization problem with objective function $f$ and solution space $S$ , the greedy choice property holds if:

$\forall$ partial solution $S_i$ , $\exists$ optimal solution $S^*$ such that $S^*$ contains the greedy choice $g_{i+1}$ made from state $S_i$

Optimal Substructure

Definition: An optimal solution to the problem contains optimal solutions to subproblems.

Mathematical Formulation: If $S^*$ is an optimal solution to problem $P$ , and $P$ can be decomposed into subproblems $P_1, P_2, ..., P_k$ , then $S^*$ contains optimal solutions $S_1^*, S_2^*, ..., S_k^*$ to these subproblems.

Classic Greedy Algorithm Examples

Activity Selection Problem

Problem Statement: Given n activities with start times sᵢ and finish times fᵢ, select the maximum number of non-overlapping activities.

Mathematical Formulation:

Input: Activities $A = \{a_1, a_2, \ldots, a_n\}$ with intervals $[s_i, f_i)$
Output: Maximum subset $S ⊆ A$ such that ∀ $a_i, a_j ∈ S$ , $[s_i, f_i) ∩ [s_j, f_j) = \varnothing$

Algorithm:

Sort activities by increasing finish time.
Iteratively pick the next activity whose start time ≥ last selected activity's finish time.
This greedy choice (earliest finishing first) yields an optimal solution.

def select_max_activities(activities):
    """
    activities: list of (start, finish) pairs representing [s, f)
    returns: list of selected (start, finish) pairs forming a maximum-size compatible set
    """
    # 1) Sort by finish time
    activities = sorted(activities, key=lambda x: x[1])
 
    selected = []
    last_finish = float("-inf")  # allows picking the first interval
 
    # 2) Greedily select non-overlapping intervals
    for s, f in activities:
        if s >= last_finish:      # [s, f) allows s == last_finish
            selected.append((s, f))
            last_finish = f
 
    return selected
 
# Example
if __name__ == "__main__":
    acts = [(1, 4), (3, 5), (0, 6), (5, 7), (8, 9), (5, 9)]
    chosen = select_max_activities(acts)
    print("Selected:", chosen)           # e.g., [(1, 4), (5, 7), (8, 9)]
    print("Maximum count:", len(chosen)) # 3

Time Complexity: $O(n \log n)$ for sorting + $O(n)$ for selection = $O(n \log n)$ Space Complexity: $O(n)$ for storing selected activities

Knapsack Problem (Fractional)

Problem Statement: Given n items with weights $w_i$ and values $v_i$ , and knapsack capacity $W$ , maximize value while respecting weight constraint. Fractional items allowed.

Mathematical Formulation: Maximize: $\sum_{i} x_{i}v_{i}$ Subject to: $\sum_{i} x_{i}w_{i} \leq W$ , where $0 \leq x_{i} \leq 1$

Greedy Strategy

Sort items by value density $v_{i} / w_{i}$ in descending order.
Take whole items while capacity allows; take a fraction of the first item that doesn't fit.

def fractional_knapsack(items, capacity):
    """
    items: list of (value, weight)
    capacity: knapsack capacity
    returns: (max_value, picks) where picks = [(value, weight, fraction_taken), ...]
    """
    # Sort by value density (value/weight), highest first
    items = sorted(items, key=lambda x: x[0] / x[1], reverse=True)
 
    value = 0.0
    picks = []
 
    for v, w in items:
        if capacity <= 0:
            break
        if w <= capacity:
            value += v
            picks.append((v, w, 1.0))
            capacity -= w
        else:
            frac = capacity / w
            value += v * frac
            picks.append((v, w, frac))
            break
 
    return value, picks
 
# Example
if __name__ == "__main__":
    items = [(60, 10), (100, 20), (120, 30)]
    W = 50
    max_val, taken = fractional_knapsack(items, W)
    print(f"Max value: {max_val:.2f}")        # 240.00
    print("Taken:", taken)                    # [(100, 20, 1.0), (120, 30, 1.0), (60, 10, 0.0)] or similar by density

Time Complexity: $O(n \log n)$ for sorting; space $O(n)$ .

Huffman Coding

Problem Statement: Design optimal prefix-free binary codes for characters based on their frequencies. Mathematical Formulation: Minimize: $Σ_{i} f_{i} * l_{i}$ where $f_{i}$ is frequency and $l_{i}$ is code length for character $i$ Greedy Strategy:

Build a min-heap of nodes (characters with frequencies).
Repeatedly extract two nodes with smallest frequencies, combine them into a new node with summed frequency, and reinsert.
Continue until one node remains (the root of the Huffman tree).
Assign binary codes by traversing the tree (left=0, right=1).

Huffman Codes Generated:

Character	Frequency	Huffman Code	Code Length
f	45	0	1
e	16	111	3
d	13	101	3
c	12	100	3
b	9	1101	4
a	5	1100	4

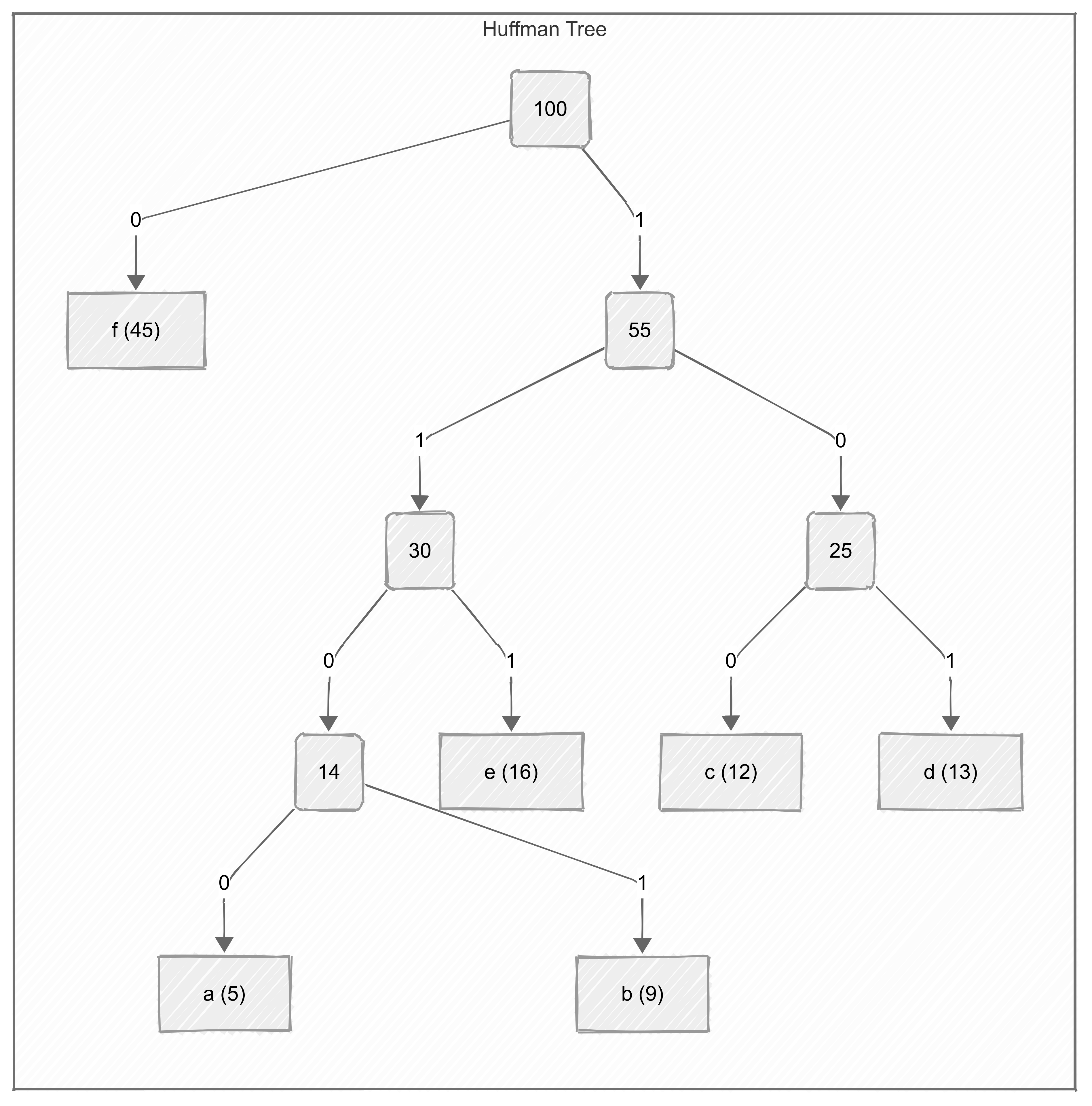
HuffmanCoding

import heapq
from collections import defaultdict
class Node:
    def __init__(self, char, freq):
        self.char = char
        self.freq = freq
        self.left = None
        self.right = None
 
    def __lt__(self, other):
        return self.freq < other.freq
def huffman_coding(frequencies):
    """
    frequencies: dict of {char: freq}
    returns: dict of {char: huffman_code}
    """
    # Build priority queue (min-heap)
    heap = [Node(char, freq) for char, freq in frequencies.items()]
    heapq.heapify(heap)
    # Build Huffman Tree
    while len(heap) > 1:
        left = heapq.heappop(heap)
        right = heapq.heappop(heap)
        merged = Node(None, left.freq + right.freq)
        merged.left = left
        merged.right = right
        heapq.heappush(heap, merged)
    root = heap[0]
    # Generate codes
    codes = {}
    def generate_codes(node, current_code):
        if node:
            if node.char is not None:
                codes[node.char] = current_code
            generate_codes(node.left, current_code + "0")
            generate_codes(node.right, current_code + "1")
    generate_codes(root, "")
    return codes
# Example
if __name__ == "__main__":
    freqs = {'a': 5, 'b': 9, 'c': 12, 'd': 13, 'e': 16, 'f': 45}
    huff_codes = huffman_coding(freqs)
    print("Huffman Codes:", huff_codes)

Time Complexity: $O(n \log n)$ for building the tree; space $O(n)$ for codes.

Minimum Spanning Tree (MST) - Prim's and Kruskal's Algorithms

Problem Statement: Given a connected, undirected graph, find a subset of edges that forms a tree including every vertex, where the total edge weight is minimized.

The algorithm is greedy because at each step, it chooses the minimum weight edge available that maintains the tree property (no cycles).

Mathematical Formulation: Minimize: $\sum_{(u,v) \in E'} w(u,v)$ where

$E'$ is the set of edges in the spanning tree
$w(u,v)$ is the weight of edge $(u,v)$

Greedy Strategies:

Prim's Algorithm: Start from an arbitrary vertex, grow the MST by adding the smallest edge that connects a vertex in the MST to a vertex outside it.

Initialize a min-heap (priority queue) with the starting vertex and its edges.
While the min-heap is not empty:
- Extract the minimum weight edge.
- If the edge connects a vertex outside the MST, add it to the MST and include the new vertex.
- Otherwise, discard the edge.

import heapq
def prim_mst(graph, start=0):
    """
    graph: adjacency list {node: [(neighbor, weight), ...]}
    start: starting vertex
    returns: list of edges in the MST and total weight
    """
    mst_edges = []
    total_weight = 0
    visited = set()
    min_heap = [(0, start, None)]  # (weight, current_node, from_node)
    while min_heap:
        weight, u, from_node = heapq.heappop(min_heap)
        if u in visited:
            continue
        visited.add(u)
        total_weight += weight
        if from_node is not None:
            mst_edges.append((from_node, u, weight))
        for v, w in graph[u]:
            if v not in visited:
                heapq.heappush(min_heap, (w, v, u))
    return mst_edges, total_weight
# Example
if __name__ == "__main__":
    graph = {
        0: [(1, 4), (2, 1)],
        1: [(0, 4), (2, 2), (3, 5)],
        2: [(0, 1), (1, 2), (3, 8)],
        3: [(1, 5), (2, 8)]
    }
    mst, weight = prim_mst(graph)
    print("MST Edges:", mst)
    print("Total Weight:", weight)

Time Complexity: $O(E \log V)$ using a priority queue; space $O(V)$ for visited set and heap.

Kruskal's Algorithm: Sort all edges by weight, and add them one by one to the MST, skipping those that would form a cycle (using Union-Find to detect cycles).

Sort edges by weight.
Initialize a Union-Find structure to track connected components.
Iterate through sorted edges:
- If the edge connects two different components, add it to the MST and union the components

class UnionFind:
    def __init__(self, size):
        self.parent = list(range(size))
        self.rank = [1] * size
 
    def find(self, u):
        if self.parent[u] != u:
            self.parent[u] = self.find(self.parent[u])
        return self.parent[u]
 
    def union(self, u, v):
        root_u = self.find(u)
        root_v = self.find(v)
        if root_u != root_v:
            if self.rank[root_u] > self.rank[root_v]:
                self.parent[root_v] = root_u
            elif self.rank[root_u] < self.rank[root_v]:
                self.parent[root_u] = root_v
            else:
                self.parent[root_v] = root_u
                self.rank[root_u] += 1
 
def kruskal_mst(edges, num_vertices):
    """
    edges: list of (weight, u, v)
    num_vertices: number of vertices in the graph
    returns: list of edges in the MST and total weight
    """
    edges.sort()  # Sort edges by weight
    uf = UnionFind(num_vertices)
    mst_edges = []
    total_weight = 0
    for weight, u, v in edges:
        if uf.find(u) != uf.find(v):
            uf.union(u, v)
            mst_edges.append((u, v, weight))
            total_weight += weight
    return mst_edges, total_weight
# Example
if __name__ == "__main__":
    edges = [
        (4, 0, 1), (1, 0, 2), (2, 1, 2),
        (5, 1, 3), (8, 2, 3)
    ]
    num_vertices = 4
    mst, weight = kruskal_mst(edges, num_vertices)
    print("MST Edges:", mst)
    print("Total Weight:", weight)

Dynamic Programming

What is Dynamic Programming? Dynamic Programming is a method for solving complex problems by breaking them down into simpler subproblems and storing the results of these subproblems to avoid redundant computations. It is particularly effective for optimization problems where the solution can be constructed from solutions to smaller subproblems. Formal Definition: A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to its subproblems. It exhibits overlapping subproblems if the same subproblems are solved multiple times during the computation of the overall solution.

Core Principles The dynamic programming paradigm operates on three fundamental principles:

Optimal Substructure: The optimal solution to a problem can be constructed from optimal solutions to its subproblems.
Overlapping Subproblems: The problem can be broken down into subproblems that

are reused multiple times.
Memoization or Tabulation: Store the results of subproblems to avoid redundant computations.

Essential Properties of Dynamic Programming

Deterministic Nature: Given the same input, a dynamic programming algorithm will always produce the same output, making it predictable and analyzable. Optimal Substructure: If a problem can be divided into subproblems, and the optimal solution to the overall problem can be constructed from the optimal solutions of its subproblems, then the problem has optimal substructure. This property is crucial for the applicability of dynamic programming. Overlapping Subproblems: If a problem can be broken down into subproblems that are solved multiple times, then the problem has overlapping subproblems. This property allows dynamic programming to store the results of these subproblems and reuse them, significantly improving efficiency. Memory Efficiency: Dynamic programming algorithms often require additional memory to store the results of subproblems, which can lead to increased space complexity. However, techniques such as space optimization can be employed to reduce memory usage in certain cases.

Classic Dynamic Programming Examples

Fibonacci Sequence

Problem Statement: Compute the n-th Fibonacci number, where each number is the sum of the two preceding ones, starting from 0 and 1. Mathematical Formulation:

Base Cases: $F(0) = 0, F(1) = 1$
Recurrence Relation: $F(n) = F(n-1) + F(n-2)$ for $n \geq 2$

# Recursive with Memoization
def fibonacci_memo(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
    return memo[n]
 
# Iterative with Tabulation
def fibonacci_tab(n):
    if n <= 1:
        return n
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]
# Space Optimized Iterative
def fibonacci_optimized(n):
    if n <= 1:
        return n
    a, b = 0, 1
    for _ in range(2, n + 1):
        a, b = b, a + b
    return b
# Example
if __name__ == "__main__":
    n = 10
    print(f"Fibonacci({n}) with memoization:", fibonacci_memo(n))
    print(f"Fibonacci({n}) with tabulation:", fibonacci_tab(n))
    print(f"Fibonacci({n}) optimized:", fibonacci_optimized(n))

0/1 Knapsack Problem

Problem Statement: Given weights and values of $n$ items, put these items in a knapsack of capacity $W$ to get the maximum total value in the knapsack. Each item can be included or excluded $(0/1)$ .

Mathematical Formulation:

Let $v_i$ be the value and $w_i$ be the weight of item
Let $K(i, w)$ be the maximum value that can be attained with a knapsack capacity $w$ using the first $i$ items.
Recurrence Relation:
- $K(0, w) = 0$ for all $w$
- $K(i, 0) = 0$ for all $i$
- $K(i, w) = K(i-1, w)$ if $w < w_i$
- $K(i, w) = max(K(i-1, w), v_i + K(i-1, w - w_i))$ if $w >= w_i$

def knapsack_01(weights, values, W):
    n = len(values)
    dp = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
    
    for i in range(1, n + 1):
        for w in range(W + 1):
            if weights[i - 1] <= w:
                dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])
            else:
                dp[i][w] = dp[i - 1][w]
    
    return dp[n][W]
# Example
if __name__ == "__main__":
    weights = [3, 4, 6, 5]
    values = [2, 3, 1, 4]
    W = 8
    print("Maximum value in Knapsack =", knapsack_01(weights, values, W))
    # Output: 6

DP table (rows = items added, columns = capacity 0-8):

items\capacity	3	4	5	6	7	8
0 (0,0)	0	0	0	0	0	0
1 (3,2)	2	2	2	2	2	2
2 (4,3)	2	3	3	3	5	5
3 (5,4)	2	3	4	4	5	6
4 (6,1)	2	3	4	4	5	6

Longest Common Subsequence (LCS)

Problem Statement: Given two sequences, find the length of the longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order but not necessarily contiguous.

Mathematical Formulation:

Let $X = x_1, x_2, \ldots, x_m$ and $Y = y_1, y_2, \ldots, y_n$
Let $L(i, j)$ be the length of LCS of $X[1..i]$ and $Y[1..j]$
Recurrence Relation:
- $L(0, j) = 0$ for all $j$
- $L(i, 0) = 0$ for all $i$
- $L(i, j) = L(i-1, j-1) + 1$ if $x_i = y_j$
- $L(i, j) = max(L(i-1, j), L(i, j-1))$ if $x_i \neq y_j$

def lcs(X, Y):
    m = len(X)
    n = len(Y)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if X[i - 1] == Y[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    return dp[m][n]
# Example
if __name__ == "__main__":
    X = "AGGTAB"
    Y = "GXTXAYB"
    print("Length of LCS is", lcs(X, Y))  # Output: 4

DP table (rows = chars of X, columns = chars of Y):

	1 (G)	2 (X)	3 (T)	4 (X)	5 (A)	6 (Y)	7 (B)
0	0	0	0	0	0	0	0
1 (A)	0	0	0	0	1	1	1
2 (G)	1	1	1	1	1	1	1
3 (G)	1	1	1	1	1	1	1
4 (T)	1	1	2	2	2	2	2
5 (A)	1	1	2	2	3	3	3
6 (B)	1	1	2	2	3	3	4

Time Complexity: $O(m \times n)$ where $m$ and $n$ are the lengths of the two sequences. Space Complexity: $O(m \times n)$ for the DP table; can be optimized to $O(\min(m, n))$ by storing only the current and previous rows.

Edit Distance (Levenshtein Distance)

Problem Statement: Given two strings, find the minimum number of operations (insertions, deletions, substitutions) required to convert one string into the other.

Mathematical Formulation:

Let $X = x_1, x_2, \ldots, x_m$ and $Y = y_1, y_2, \ldots, y_n$
Let $D(i, j)$ be the edit distance between $X[1..i]$ and $Y[1..j]$
Recurrence Relation:
- $D(0, j) = j$ for all $j$ (all insertions)
- $D(i, 0) = i$ for all $i$
- $D(i, j) = D(i-1, j-1)$ if $x_i = y_j$
- $D(i, j) = 1 + \min(D(i-1, j), D(i, j-1), D(i-1, j-1))$ if $x_i \neq y_j$

def edit_distance(X, Y):
    m = len(X)
    n = len(Y)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    for i in range(m + 1):
        for j in range(n + 1):
            if i == 0:
                dp[i][j] = j  # Insert all j characters
            elif j == 0:
                dp[i][j] = i  # Remove all i characters
            elif X[i - 1] == Y[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]
            else:
                dp[i][j] = 1 + min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])
    return dp[m][n]
# Example
if __name__ == "__main__":
    X = "kitten"
    Y = "sitting"
    print("Edit Distance is", edit_distance(X, Y))  # Output: 3

Time Complexity: $O(m \times n)$ where $m$ and $n$ are the lengths of the two strings. Space Complexity: $O(m \times n)$ for the DP table; can be optimized to $O(\min(m, n))$ by storing only the current and previous rows.

Graph Data Structures and Algorithms

Graph Data Structures

Graphs are abstract data types that consist of a set of nodes (or vertices) and a set of edges connecting pairs of nodes. They are used to model relationships and connections in various domains, such as social networks, transportation systems, and communication networks.

Graph Representations

Adjacency Matrix: A 2D array where the cell at row i and column j indicates the presence (and possibly weight) of an edge between vertex i and vertex j. This representation is efficient for dense graphs but can be space-inefficient for sparse graphs.

Space Complexity: $O(V^2)$ where $V$ is the number of vertices.
Time Complexity: $O(1)$ for edge look-up, $O(V)$ for iterating over neighbors.

class GraphAdjMatrix:
    def __init__(self, vertices):
        self.V = vertices
        self.adj_matrix = [[0] * vertices for _ in range(vertices)]
 
    def add_edge(self, u, v, weight=1):
        self.adj_matrix[u][v] = weight
        self.adj_matrix[v][u] = weight  # For undirected graph
 
    def remove_edge(self, u, v):
        self.adj_matrix[u][v] = 0
        self.adj_matrix[v][u] = 0
 
    def display(self):
        for row in self.adj_matrix:
            print(row)

Adjacency List: A list where each vertex has a list of its adjacent vertices (and possibly edge weights). This representation is more space-efficient for sparse graphs.

Space Complexity: $O(V + E)$ where $E$ is the number of edges.
Time Complexity: $O(V)$ for edge look-up, $O(degree(V))$ for iterating over neighbors.

class GraphAdjList:
     def __init__(self):
          self.adj_list = {}
 
     def add_edge(self, u, v, weight=1):
          if u not in self.adj_list:
            self.adj_list[u] = []
          if v not in self.adj_list:
            self.adj_list[v] = []
          self.adj_list[u].append((v, weight))
          self.adj_list[v].append((u, weight))  # For undirected graph
 
     def remove_edge(self, u, v):
          if u in self.adj_list:
            self.adj_list[u] = [pair for pair in self.adj_list[u] if pair[0] != v]
          if v in self.adj_list:
            self.adj_list[v] = [pair for pair in self.adj_list[v] if pair[0] != u]
 
     def display(self):
          for key in self.adj_list:
            print(f"{key}: {self.adj_list[key]}")

Some important Alogorithms

Kadane's Algorithm : Maximum Subarray Sum in an Array

The intuition behind Kadane's Algorithm is to iterate through the array while maintaining a running sum of the current subarray. If the running sum becomes negative, it is reset to zero. The maximum sum encountered during the iteration is the result.

Steps:

Iterate over the array with a loop (index i).
Add each element to a running sum and update the maximum sum when the running sum is larger.
If the running sum becomes negative, reset it to 0 since continuing from a negative sum cannot improve the result.

def maxSubarraySum(arr, n):
    maximum_sum = float('-inf')
    sum = 0
    start = 0
    subarrayStartIndex, subarrayEndIndex = -1, -1
    for i in range(n):
        if sum == 0:
            start = i
        sum += arr[i]
        if sum > maximum_sum:
            maximum_sum = sum
            subarrayStartIndex = start
            subarrayEndIndex = i
        # If sum < 0: discard the sum calculated
        if sum < 0:
            sum = 0
 
    print("The subarray is: [", end="")
    for i in range(subarrayStartIndex, subarrayEndIndex + 1):
        print(arr[i], end=" ")
    print("]")
    return maximum_sum
 
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
n = len(arr)
maxSum = maxSubarraySum(arr, n)
print("The maximum subarray sum is:", maxSum)

Note: I'm continually adding and updating context as I learn. Please check back for updates.

See all blogs